LL =
RL =
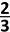 ≈ 0,67
≈ 0,67
LL > RL → O.K.
| Te bewijzen : | ||
| Bewijs : | ||
| Deel I : |
Voor de kleinste n-waarde, nl. 2 is LL = RL = 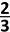 ≈ 0,67 ≈ 0,67
LL > RL → O.K. |
| Deel II : | Gegeven : |
|
| Te bewijzen : |
| |
| Bewijs : |
Uit het gegeven volgt ook nog | |
| __
Nu valt er te bewijzen dat | ||
| __ of (na ×3k+1) 3.kk(k+1) − (k+1)k+1 > 0 | ||
| __ of (na : (k+1) ) 3.kk − (k+1)k > 0 | ||
| __
of (na : kk ) | ||
| __
of | ||
| __
of | ||
|
|